https://www.squaring-the-circle.com/en/
square the circle with ruler and compasses only
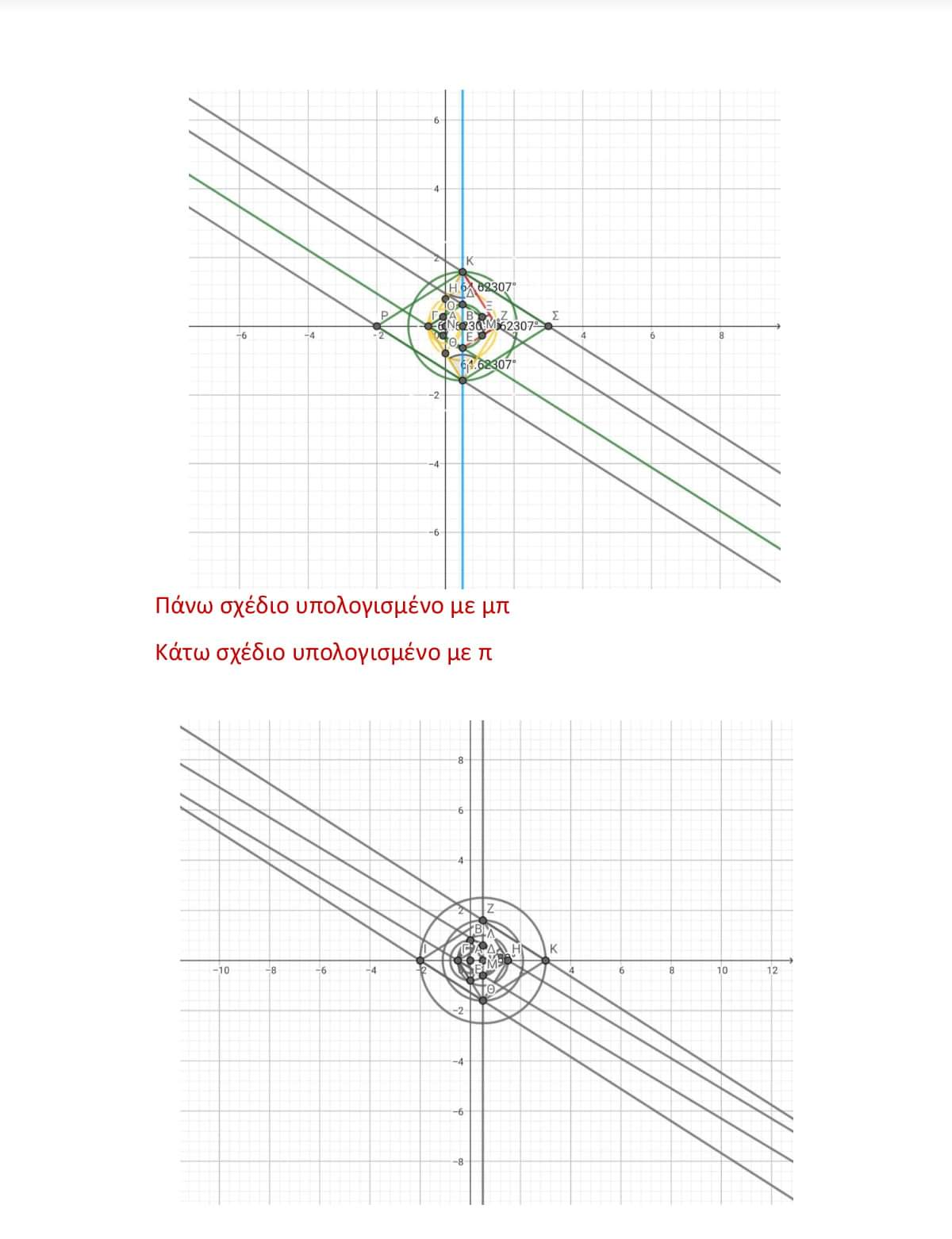
Η μόνη τιμή ΜΠ σε κατασκευή που τετραγωνίζει το κύκλο, και μας δίνει εφαρμογή.
Κατασκευή τετραγωνισμού του κύκλου σύμφωνα με την ευκλείδειο γεωμετρία, μόνο με κανόνα και διαβήτη.
Από τη Wikipedia
(Τετραγωνίζω τον κύκλο σημαίνει ότι κατασκευάζω, με γεωμετρική ή αλγεβρική μέθοδο, ένα τετράγωνο με εμβαδόν ίσο με το εμβαδόν του κύκλου.
Η δυσκολία του προβλήματος συνίσταται σε δύο περιορισμούς που έθεσαν σε αυτό οι αρχαίοι Έλληνες μαθηματικοί. Πιο συγκεκριμένα, για να θεωρηθεί αποδεκτή μία λύση του προβλήματος, σε αυτήν θα πρέπει:[1]
Να χρησιμοποιηθεί μόνο κανόνας και διαβήτης, προκειμένου η απόδειξη να ανάγεται πλήρως στα θεωρήματα του Ευκλείδη, και
Να μην πραγματοποιείται μετά από άπειρο αριθμό βημάτων.
Αποδεικνύεται ότι το πρόβλημα του τετραγωνισμού του κύκλου επιλύεται εύκολα αν άρουμε οποιονδήποτε από αυτούς τους δύο περιορισμούς.)
Η απόδειξη ότι δεν μπορεί να κατασκευαστή τετράγωνο ιδίου εμβαδού με το εμβαδόν του κύκλου, και ο αριθμός π απορρέουν μετά άπειρο αριθμό βημάτων και σύμφωνα με τον Ευκλείδη τίποτε από τα δυο δεν είναι αποδεκτά . Ούτε ο π ως λύση ούτε η απόδειξη ως λύση. Αλλά μόνο στη θεωρητική γεωμετρία. .
Σύμφωνα με την ευκλείδειο γεωμετρία το Πυθαγόρειο και τη λύση του Δεινόστρατου.
(ο Δεινόστρατος είπε. αν κρατήσω την ακτίνα κάθετη και κυλούσα τον κύκλο μέχρι να γίνει ευθεία. το τρίγωνο κεντρο ρ π (ΑΜΠ)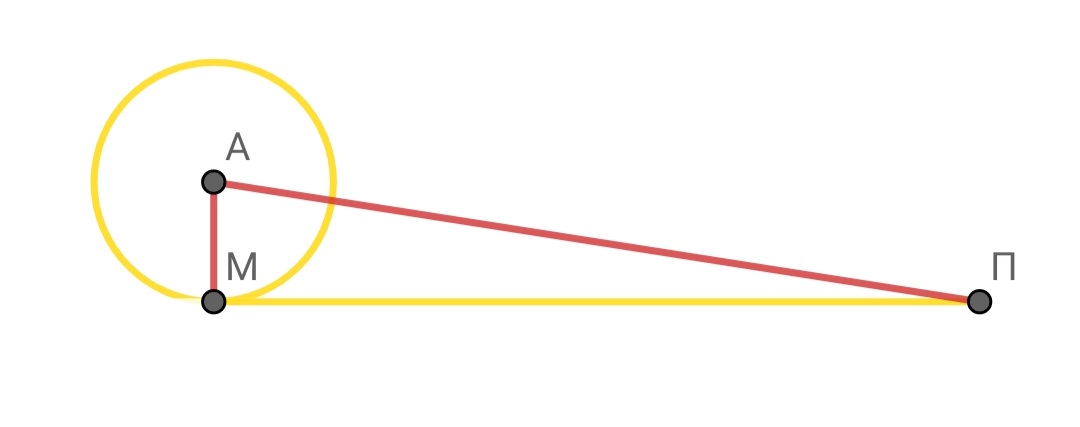
θα ήταν ίσο με το εμβαδόν του κύκλου... δηλαδή ακτίνα επι περίμετρο δια δυο... οπότε και ακτίνα επι 1/2 περιμέτρου ισούται με το εμβαδόν. οπότε και με αλλο σχήμα ... διάμετρο επι 1/2 περιμέτρου δια δύο θα έχω ρόμβο ιδίου εμβαδού με του κύκλου.)
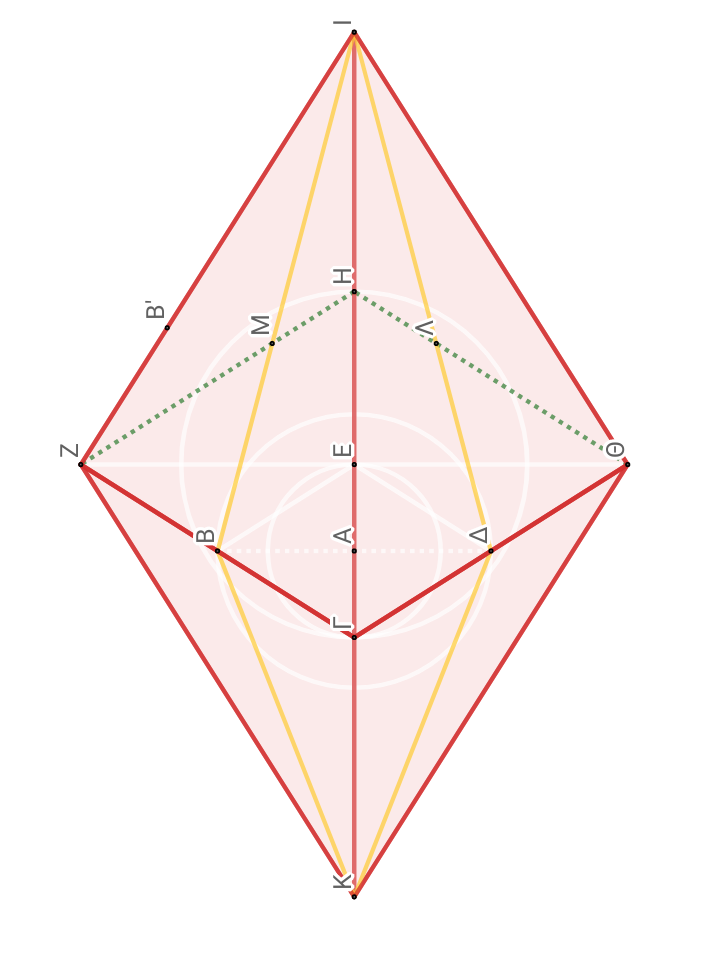
Κατασκευάζω ρόμβο και κύκλο ιδίου εμβαδού μόνο με κανόνα και διαβήτη.Το σχήμα αναπτύσσεται από το αρχικό εμβαδού ¼ μπ τέσσερις φορές σε εμβαδόν μπ . Επόμενο βήμα αναπτύσσεται όσο ¼ μπ^2 σε εμβαδόν μπ × ¼ μπ^2 και τελικό βήμα θα διαιρέσω από εμβαδόν μπ όσο ¼ μπ^2 σε εμβαδόν 4/μπ (περιμέτρου 4 και διαμέτρου 4/μπ)
Κατασκευάζω μόνο με κανόνα και διαβήτη σύμφωνα με της παράλληλους χαράζουμε πλευρές ρόμβου και διαμέτρους με γωνίες 90° από τις κορφές του ρόμβου μπ χαράσσουμε τους επόμενους.
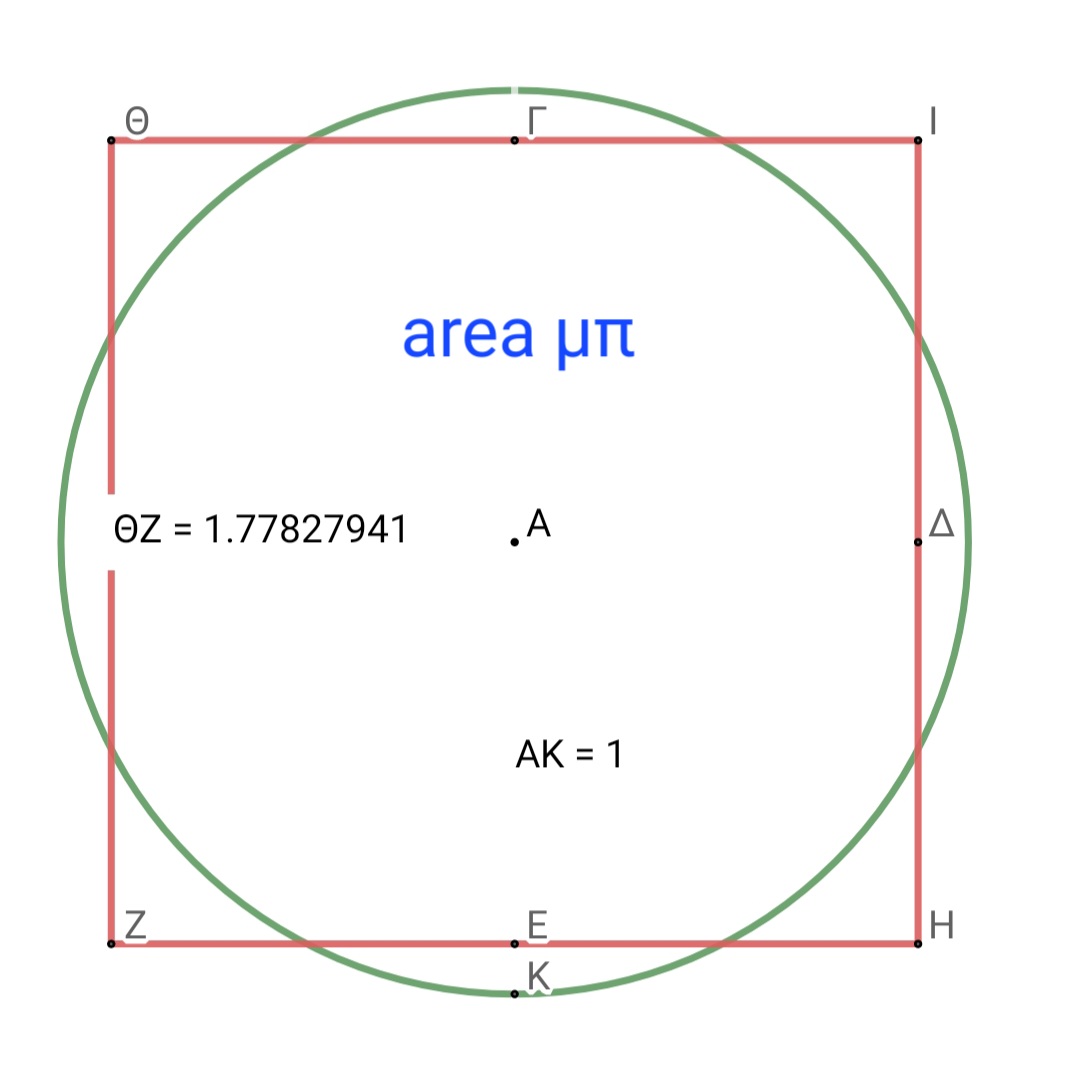
Η ακριβής τιμή μπ επαληθεύεται στο τελικό βήμα , όπου εκεί έχουμε περίμετρο ίση με τέσσερα και η διάμετρος του χαράσσεται με την παράλληλη φέρνοντας κάθετη από τη πλευρά ρόμβου εμβαδού μπ
και μπορούμε να υπολογίσουμε το λάθος και την απόκλιση οποίας άλλης τιμής.
(Όπου ΜΠ=Χ= περίμετρο κύκλου με διάμετρο ένα
ΒΗΜΑΤΑ ΚΑΤΑΣΚΕΥΗΣΗ κατασκευή δημιουργείται με την υπόθεση ΗΑ και επαληθεύεται στο τελικό βήμα με τη ΒΕ.
Η κατασκευή είναι άγνωστη και χρειάζεται μελέτη για να κατανοηθεί.