https://www.geogebra.org/classic/tracmaga
Bouras 4D Geometry
A geometry-first canonical framework in which the primary geometric configuration defines all invariant structures, while algebraic expressions serve only as derived representations.
Primary Reference
Technical note published on Zenodo
Foundational Work — Version 6
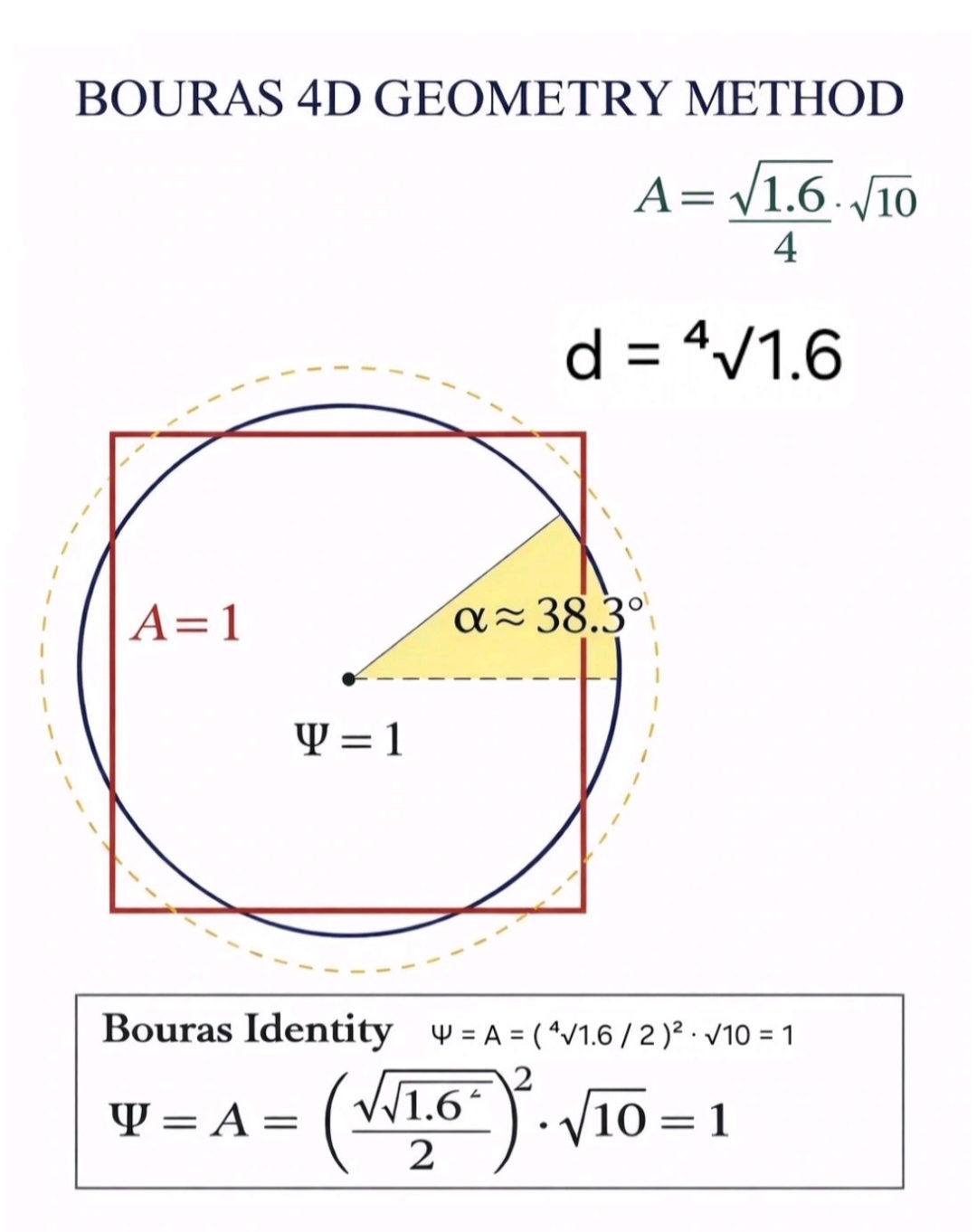
Quadrature of the Circle via Dimensionless Periodic Normalization
Conference paper, Version 6
Zenodo (January 18, 2026)
This work constitutes the most complete and mature formulation of the Bouras 4D Geometry Method to date.
It presents a fully dimensionless, axiomatic, and periodic geometric normalization framework, establishing the quadrature of the circle as a consequence of invariant geometric structure rather than numerical approximation.
The formulation introduces:
A geometry-first normalization principle
A periodic invariant framework independent of algebraic parametrization
A constructive geometric process grounded in canonical configuration
This version serves as the primary reference implementation of the method.
System-Level and Structural Overview
This work provides a system-level and structural description of the Bouras 4D Geometry Method, clarifying its foundational architecture, invariant components, and normalization logic.
It establishes the method as a unified geometric framework in which structural consistency, periodic invariance, and canonical configuration precede algebraic formalization.
The document functions as an intermediate reference between the foundational construction and the canonical interpretation, detailing how individual components integrate into a coherent geometric system.
🔗 https://zenodo.org/records/18371594
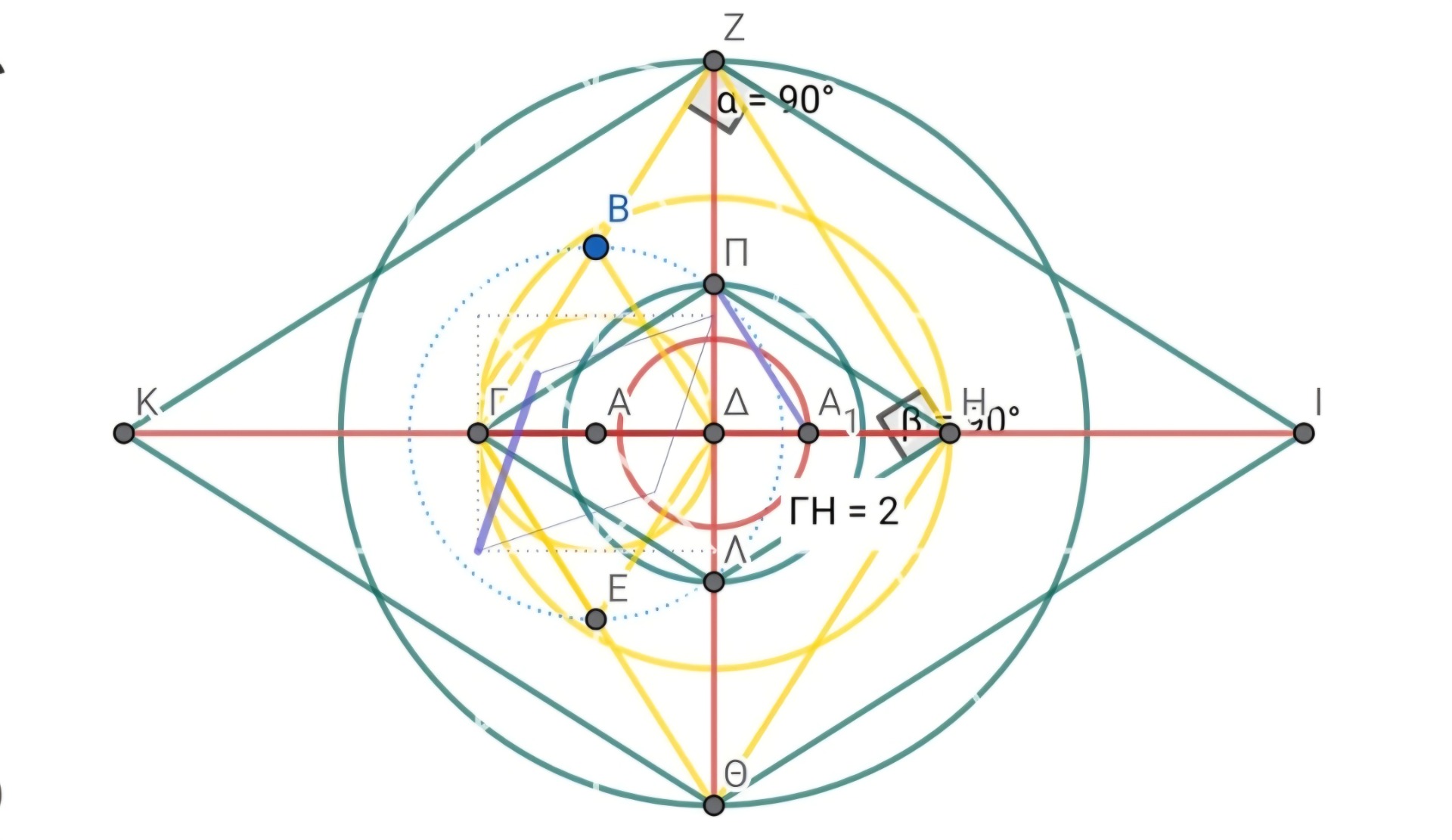
Foundational Construction of the Bouras 4D Geometry Method
This work presents the foundational geometric construction of the Bouras 4D Geometry Method, establishing the primary canonical configuration from which all invariant structures arise.
The construction is purely geometric and deterministic, independent of algebraic approximation or numerical fitting. All subsequent formulations, normalizations, and invariants derive from this initial configuration.
This document serves as the geometric foundation upon which later system-level descriptions and canonical interpretations are built.
External Peer-Reviewed Publication
An independent peer-reviewed publication presenting constructive steps and geometric methodology related to the Bouras 4D Geometry framework.
IOSR Journal of Mathematics (January 2024):https://www.iosrjournals.org/iosr-jm/papers/Vol20-issue1/Ser-1/D2001012325.pdf
This page serves as the central reference for the Bouras 4D Geometry Method.
All published technical notes, figures, and formal descriptions are archived on Zenodo and linked via their respective DOIs.
The website provides an accessible overview, while the Zenodo records constitute the authoritative scientific references.